Harmonic Motion Equation   조화 진동 방정식, 조화 운동 방정식

1. (단순) 조화진동 운동방정식의 표준형

  ㅇ 2차 시스템(2계 미분방정식) 형태를 띔
      
[# \ddot{Ψ} + ω^2_o Ψ = 0 #]
     - 2차 미분항 {#\ddot{Ψ}#} : 가속도 항
        . 여기서, 중요 성질을 갖는 함수로써, 고유함수가 있음      ☞ 고유 함수(Eigenfunction) 참조
           .. 2회 미분하여 원래의 -ωo2 상수배가 되는 함수({#\ddot{Ψ}= -ω^2_oΨ#})로써,
           .. 이같은 고유함수가 입력이 될 때, 그 출력은 그 고유함수의 복소 상수배가 됨
           .. 이 함수의 특징으로는, 입출력 주파수 성분이 변화 없음 (그대로임)
     - 1차 미분항 {#\dot{Ψ}#} : 감쇠 항  =>  위 단순 조화 운동방정식에는 `없음`
        . 따라서, `비감쇠 자유진동`을 의미함      ☞ 비감쇠 자유진동(Undamped Free Vibration) 참조
     - {#ω^2_o Ψ#} : 상수 비례항
     - ωo : 자연주파수
     - Ψ : 변위, 시간 t의 함수 Ψ(t) 

  ※ [명칭]  위 식을 단순 조화 미분방정식 이라고도 함
     - 사인함수 또는 코사인함수 처럼 주기적 운동을 표현 함


2. (단순) 조화진동 운동방정식의 유도 例)

   

  ㅇ 운동방정식 유도
     - 후크의 법칙 (F=-kx)을 뉴튼의 운동법칙 (F=ma)에 대입하면,
       
       
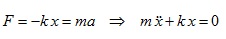
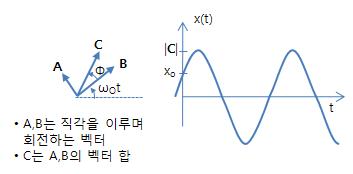
        .  m : 질량(Mass) [kg]
        .  k : 스프링상수 또는 탄성계수 또는 강성도
        .  ωo = √k/m : 비제동 자연주파수(Undamped Natural Frequency) [rad/sec] 


3. (단순) 조화진동 운동방정식의 특징

  ㅇ (진동)  :  선형 복원력을 받는 질량의 진동
     - 힘의 크기 : 평형점으로부터 변위에 비례하는 힘을 받음 => (선형 복원력)
     - 힘의 방향 : 변위에 반대방향 => (항상 평형점을 향함)
     * 변위가 커질수록 그 반대 방향으로의 힘이 커짐

  ㅇ (결합)  :  두 요소가 결합된 진동
     - 관성 요소 : 관성 질량 m  (운동에너지를 저장 및 방출)
     - 탄성 요소 : 스프링 같은 탄성체 (위치에너지를 저장 및 방출)
        . 위치에너지 : 스프링 같은 탄성체를 변형시키는데 소요된 일

  ㅇ (가속도)  :  변위에 비례적이나, 방향이 반대방향 
     - (즉, 변위 보다 가속도의 위상차가 180˚ 빠름)
     -  F = -kx = ma 에서  a = -(k/m)x 

  ㅇ (속도)  :  변위가 0 일 때 가장 크고, 변위가 가장 클 때 0 이됨
     - (즉, 변위 보다 위상차가 90˚ 빠름)

  ㅇ (주파수)  :  진동 주파수
     - 만일, k(탄성계수)가 감소하거나 m(질량)이 증가하면, 
     - 자연주파수(고유 진동수)도 감소하게 됨
     - ωo = √k/m


4. (단순) 조화운동 운동방정식(미분방정식)의 해(解)

  ㅇ 미분방정식의 보조방정식(특성방정식)
     - λ2 + 0 λ + ωo2 = 0
        . 보조방정식(특성방정식) :  선형 동차 미분방정식 해와 관련된 대수적 방정식
        . 보조방정식 근(根) : λ=±jωo 

  ㅇ 미분방정식의 일반해
     -   x(t) = A cos ωot + B sin ωot
              = C sin (ωot + φ)
              = C1ejω。t + C2e-jω。t
        . 변위가 시간의 조화함수(사인 또는 코사인함수, 또는 지수함수)로 표현됨

  ㅇ 2개의 미지의 상수가 있음
     -  A : 코사인함수 진폭, B  : 사인함수 진폭
     -  또는,  C : 진폭변위, φ : 위상편이

  ㅇ 만일, 초기조건 x(0)=xo, x'(0)=vo 이 주어지면,
     -  x(t) = xo cos ωot + (vo/ωo) sin ωot


5. (단순) 조화운동 운동방정식 해(解)의 모양

   

1. ▷ Top (분류 펼침) ^New     :     1,592개 분류    6,516건 해설 검색 펼침